Algorithm Descriptions

Captum is a library within which different interpretability methods can be implemented. The Captum team welcomes any contributions in the form of algorithms, methods or library extensions!

The attribution algorithms in Captum are separated into three groups, primary attribution, layer attribution and neuron attribution, which are defined as follows:

Primary Attribution: Evaluates contribution of each input feature to the output of a model.
Layer Attribution: Evaluates contribution of each neuron in a given layer to the output of the model.
Neuron Attribution: Evaluates contribution of each input feature on the activation of a particular hidden neuron.

Below is a short summary of the various methods currently implemented for primary, layer, and neuron attribution within Captum, as well as noise tunnel, which can be used to smooth the results of any attribution method.

Beside attribution algorithms Captum also offers metrics to estimate the trustworthiness of model explanations. Currently we offer infidelity and sensitivity metrics that help us to estimate the goodness of explanations.

Primary Attribution

Integrated Gradients

Integrated gradients represents the integral of gradients with respect to inputs along the path from a given baseline to input. The integral can be approximated using a Riemann Sum or Gauss Legendre quadrature rule. Formally, it can be described as follows:

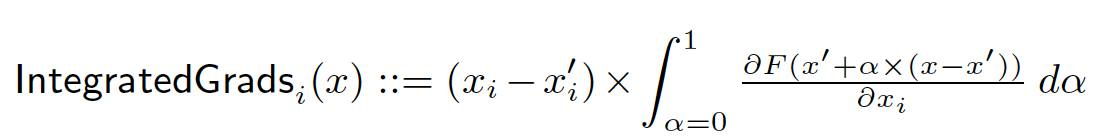IG_eq1 Integrated Gradients along the i - th dimension of input X. Alpha is the scaling coefficient. The equations are copied from the original paper.

The cornerstones of this approach are two fundamental axioms, namely sensitivity and implementation invariance. More information regarding these axioms can be found in the original paper.

To learn more about Integrated Gradients, visit the following resources:

Original paper

Gradient SHAP

Gradient SHAP is a gradient method to compute SHAP values, which are based on Shapley values proposed in cooperative game theory. Gradient SHAP adds Gaussian noise to each input sample multiple times, selects a random point along the path between baseline and input, and computes the gradient of outputs with respect to those selected random points. The final SHAP values represent the expected value of gradients * (inputs - baselines).

The computed attributions approximate SHAP values under the assumptions that the input features are independent and that the explanation model is linear between the inputs and given baselines.

To learn more about GradientSHAP, visit the following resources:

DeepLIFT

DeepLIFT is a back-propagation based approach that attributes a change to inputs based on the differences between the inputs and corresponding references (or baselines) for non-linear activations. As such, DeepLIFT seeks to explain the difference in the output from reference in terms of the difference in inputs from reference. DeepLIFT uses the concept of multipliers to "blame" specific neurons for the difference in output. The definition of a multiplier is as follows (from original paper): 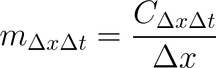deepLIFT_eq1 x is the input neuron with a difference from reference Δx, and t is the target neuron with a difference from reference Δt. C is then the contribution of Δx to Δt.

Like partial derivatives (gradients) used in back propagation, multipliers obey the Chain Rule. According to the formulations proposed in this paper. DeepLIFT can be overwritten as the modified partial derivatives of output of non-linear activations with respect to their inputs.

Currently, we only support Rescale Rule of DeepLIFT Algorithms. RevealCancel Rule will be implemented in later releases.

To learn more about DeepLIFT, visit the following resources:

DeepLIFT SHAP

DeepLIFT SHAP is a method extending DeepLIFT to approximate SHAP values, which are based on Shapley values proposed in cooperative game theory. DeepLIFT SHAP takes a distribution of baselines and computes the DeepLIFT attribution for each input-baseline pair and averages the resulting attributions per input example.

DeepLIFT's rules for non-linearities serve to linearize non-linear functions of the network, and the method approximates SHAP values for the linearized version of the network. The method also assumes that the input features are independent.

To learn more about DeepLIFT SHAP, visit the following resources:

SHAP paper

Saliency

Saliency is a simple approach for computing input attribution, returning the gradient of the output with respect to the input. This approach can be understood as taking a first-order Taylor expansion of the network at the input, and the gradients are simply the coefficients of each feature in the linear representation of the model. The absolute value of these coefficients can be taken to represent feature importance.

To learn more about Saliency, visit the following resources:

Original paper

Input X Gradient

Input X Gradient is an extension of the saliency approach, taking the gradients of the output with respect to the input and multiplying by the input feature values. One intuition for this approach considers a linear model; the gradients are simply the coefficients of each input, and the product of the input with a coefficient corresponds to the total contribution of the feature to the linear model's output.

Guided Backpropagation and Deconvolution

Guided backpropagation and deconvolution compute the gradient of the target output with respect to the input, but backpropagation of ReLU functions is overridden so that only non-negative gradients are backpropagated. In guided backpropagation, the ReLU function is applied to the input gradients, and in deconvolution, the ReLU function is applied to the output gradients and directly backpropagated. Both approaches were proposed in the context of a convolutional network and are generally used for convolutional networks, although they can be applied generically.

To learn more about Guided Backpropagation, visit the following resources:

Original paper

To learn more about Deconvolution, visit the following resources:

Guided GradCAM

Guided GradCAM computes the element-wise product of guided backpropagation attributions with upsampled (layer) GradCAM attributions. GradCAM attributions are computed with respect to a given layer, and attributions are upsampled to match the input size. This approach is designed for convolutional neural networks. The chosen layer is often the last convolutional layer in the network, but any layer that is spatially aligned with the input can be provided.

Guided GradCAM was proposed by the authors of GradCAM as a method to combine the high-resolution nature of Guided Backpropagation with the class-discriminative advantages of GradCAM, which has lower resolution due to upsampling from a convolutional layer.

To learn more about Guided GradCAM, visit the following resources:

Feature Ablation

Feature ablation is a perturbation based approach to compute attribution, involving replacing each input feature with a given baseline / reference value (e.g. 0), and computing the difference in output. Input features can also be grouped and ablated together rather than individually. This can be used in a variety of applications. For example, for images, one can group an entire segment or region and ablate it together, measuring the importance of the segment (feature group).

Feature Permutation

Feature permutation is a perturbation based approach which takes each feature individually, randomly permutes the feature values within a batch and computes the change in output (or loss) as a result of this modification. Like feature ablation, input features can also be grouped and shuffled together rather than individually. Note that unlike other algorithms in Captum, this algorithm only provides meaningful attributions when provided with a batch of multiple input examples, as opposed to other algorithms, where a single example is sufficient.

To learn more about Feature Permutation, visit the following resources:

Interpretable ML Book

Occlusion

Occlusion is a perturbation based approach to compute attribution, involving replacing each contiguous rectangular region with a given baseline / reference, and computing the difference in output. For features located in multiple regions (hyperrectangles), the corresponding output differences are averaged to compute the attribution for that feature. Occlusion is most useful in cases such as images, where pixels in a contiguous rectangular region are likely to be highly correlated.

To learn more about Occlusion (also called grey-box / sliding window method), visit the following resources:

Shapley Value Sampling

Shapley value is an attribution method based on a concept from cooperative game theory. This method involves taking each permutation of the input features and adding them one-by-one to a given baseline. The output difference after adding each feature corresponds to its contribution, and these differences are averaged over all permutations to obtain the attribution.

Since this method is extremely computationally intensive for larger numbers of features, we also implement Shapley Value Sampling, where we sample some random permutations and average the marginal contribution of features based on these permutations. Like feature ablation, input features can also be grouped and added together rather than individually.

To learn more about Shapley Value Sampling, visit the following resources:

Lime

Lime is an interpretability method that trains an interpretable surrogate model by sampling data points around a specified input example and using model evaluations at these points to train a simpler interpretable 'surrogate' model, such as a linear model.

We offer two implementation variants of this method, LimeBase and Lime. LimeBase provides a generic framework to train a surrogate interpretable model. This differs from most API of other attribution methods, since the method returns a representation of the interpretable model (e.g. coefficients of the linear model). On the other hand, Lime provides a more specific implementation than LimeBase in order to expose a consistent API with other perturbation-based algorithms.

To learn more about Lime, visit the following resources:

Original paper

KernelSHAP

Kernel SHAP is a method that uses the LIME framework to compute Shapley Values. Setting the loss function, weighting kernel and regularization terms appropriately in the LIME framework allows theoretically obtaining Shapley Values more efficiently than directly computing Shapley Values.

To learn more about KernelSHAP, visit the following resources:

Original paper

Layer Attribution

Layer Conductance

Conductance combines the neuron activation with the partial derivatives of both the neuron with respect to the input and the output with respect to the neuron to build a more complete picture of neuron importance.

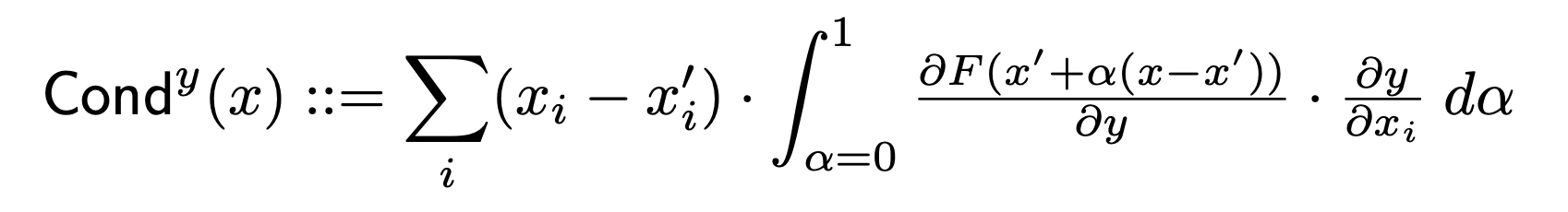
Conductance builds on Integrated Gradients (IG) by looking at the flow of IG attribution which occurs through the hidden neuron. The formal definition of total conductance of a hidden neuron y (from the original paper) is as follows: conductance_eq1

For more efficient computation of layer conductance, we use the idea presented in this paper to avoid computing the gradient of each neuron with respect to the input.

To learn more about Conductance, visit the following resources:

Internal Influence

Internal Influence approximates the integral of gradients with respect to a particular layer along the path from a baseline input to the given input. This method is similar to applying integrated gradients, integrating the gradient with respect to the layer (rather than the input).

To learn more about Internal Influence, visit the following resources:

Original Paper

Layer Activation

Layer Activation is a simple approach for computing layer attribution, returning the activation of each neuron in the identified layer.

Layer Gradient X Activation

Layer Gradient X Activation is the analog of the Input X Gradient method for hidden layers in a network. It element-wise multiplies the layer's activation with the gradients of the target output with respect to the given layer.

GradCAM

GradCAM is a layer attribution method designed for convolutional neural networks, and is usually applied to the last convolutional layer. GradCAM computes the gradients of the target output with respect to the given layer, averages for each output channel (dimension 2 of output), and multiplies the average gradient for each channel by the layer activations. The results are summed over all channels and a ReLU is applied to the output, returning only non-negative attributions.

This procedure sums over the second dimension (# of channels), so the output of GradCAM attributions will have a second dimension of 1, but all other dimensions will match that of the layer output.

Although GradCAM directly attributes the importance of different neurons in the target layer, GradCAM is often used as a general attribution method. To accomplish this, GradCAM attributions are upsampled and viewed as a mask to the input, since a convolutional layer output generally matches the input image spatially.

To learn more about GradCAM, visit the following resources:

Layer Integrated Gradients

Layer integrated gradients represents the integral of gradients with respect to the layer inputs / outputs along the straight-line path from the layer activations at the given baseline to the layer activation at the input.

To learn more about Integrated Gradients, see this section above.

Layer GradientSHAP

Layer GradientSHAP is the analog of GradientSHAP for a particular layer. Layer GradientSHAP adds Gaussian noise to each input sample multiple times, selects a random point along the path between baseline and input, and computes the gradient of the output with respect to the identified layer. The final SHAP values approximate the expected value of gradients * (layer activation of inputs - layer activation of baselines).

To learn more about Gradient SHAP, see this section above.

Layer DeepLIFT

Layer DeepLIFT is the analog of the DeepLIFT method for hidden layers in a network.

To learn more about DeepLIFT, see this section above.

Layer DeepLIFT SHAP

Layer DeepLIFT SHAP is the analog of DeepLIFT SHAP for a particular layer. Layer DeepLIFT SHAP takes a distribution of baselines and computes the Layer DeepLIFT attribution for each input-baseline pair and averages the resulting attributions per input example.

To learn more about DeepLIFT SHAP, see this section above.

Layer Feature Ablation

Layer feature ablation is the analog of feature ablation for an identified layer input or output. It is a perturbation based approach to compute attribution, involving replacing each value in the identified layer with a given baseline / reference value (e.g. 0), and computing the difference in output. Values within the layer can also be grouped and ablated together rather than individually.

Neuron Attribution

Neuron Conductance

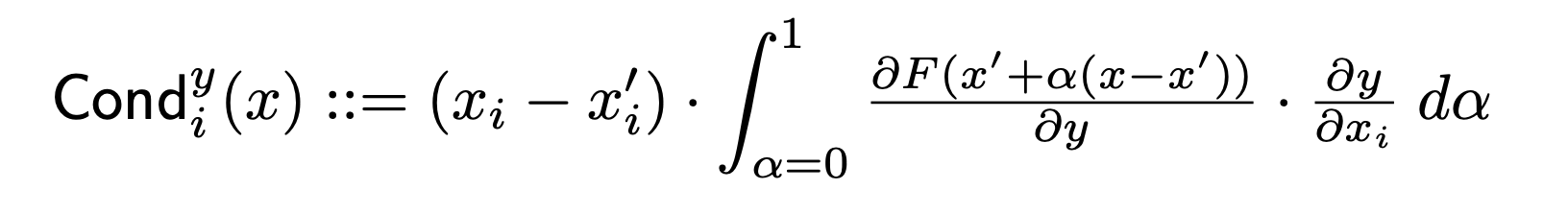
Conductance for a particular neuron builds on Integrated Gradients (IG) by looking at the flow of IG attribution from each input through the particular neuron. The formal definition of conductance of neuron y for the attribution of input i (from the original paper) is as follows: conductance_eq2

Note that based on this definition, summing the neuron conductance (over all input features) always equals the layer conductance for the particular neuron.

To learn more about Conductance, visit the following resources:

Neuron Gradient

Neuron gradient is the analog of the saliency method for a particular neuron in a network. It simply computes the gradient of the neuron output with respect to the model input. Like Saliency, this approach can be understood as taking a first-order Taylor expansion of the neuron's output at the given input, and the gradients correspond to the coefficients of each feature in the linear representation of the model.

Neuron Integrated Gradients

Neuron Integrated Gradients approximates the integral of input gradients with respect to a particular neuron along the path from a baseline input to the given input. This method is equivalent to applying integrated gradients considering the output to be simply the output of the identified neuron.

To learn more about Integrated Gradients, see this section above.

Neuron Guided Backpropagation and Deconvolution

Neuron guided backpropagation and neuron deconvolution are the analogs of guided backpropagation and deconvolution for a particular neuron.

To learn more about Guided Backpropagation and Deconvolution, see this section above.

Neuron GradientSHAP

Neuron GradientSHAP is the analog of GradientSHAP for a particular neuron. Neuron GradientSHAP adds Gaussian noise to each input sample multiple times, selects a random point along the path between baseline and input, and computes the gradient of the target neuron with respect to each selected random points. The final SHAP values approximate the expected value of gradients * (inputs - baselines).

To learn more about GradientSHAP, see this section above.

Neuron DeepLIFT

Neuron DeepLIFT is the analog of the DeepLIFT method for a particular neuron.

To learn more about DeepLIFT, see this section above.

Neuron DeepLIFT SHAP

Neuron DeepLIFT SHAP is the analog of DeepLIFT SHAP for a particular neuron. Neuron DeepLIFT SHAP takes a distribution of baselines and computes the Neuron DeepLIFT attribution for each input-baseline pair and averages the resulting attributions per input example.

To learn more about DeepLIFT SHAP, see this section above.

Neuron Feature Ablation

Neuron feature ablation is the analog of feature ablation for a particular neuron. It is a perturbation based approach to compute attribution, involving replacing each input feature with a given baseline / reference value (e.g. 0), and computing the difference in the target neuron's value. Input features can also be grouped and ablated together rather than individually. This can be used in a variety of applications. For example, for images, one can group an entire segment or region and ablate it together, measuring the importance of the segment (feature group).

Noise Tunnel

Noise Tunnel is a method that can be used on top of any of the attribution methods. Noise tunnel computes attribution multiple times, adding Gaussian noise to the input each time, and combines the calculated attributions based on the chosen type. The supported types for noise tunnel are:

Smoothgrad: The mean of the sampled attributions is returned. This approximates smoothing the given attribution method with a Gaussian Kernel.
Smoothgrad Squared: The mean of the squared sample attributions is returned.
Vargrad: The variance of the sample attributions is returned.

To learn more about Noise Tunnel methods, visit the following resources:

Metrics

Infidelity

Infidelity measures the mean squared error between model explanations in the magnitudes of input perturbations and predictor function's changes to those input perturbtaions. Infidelity is defined as follows: 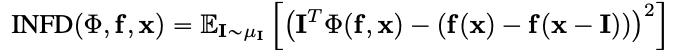infidelity_eq It is derived from the completeness property of well-known attribution algorithms, such as Integrated Gradients, and is a computationally more efficient and generalized notion of Sensitivy-n. The latter measures correlations between the sum of the attributions and the differences of the predictor function at its input and fixed baseline. More details about the Sensitivity-n can be found here: https://arxiv.org/abs/1711.06104 More details about infidelity measure can be found here:

Original paper

Sensitivity

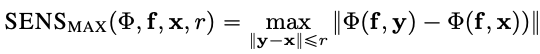Sensitivity measures the degree of explanation changes to subtle input perturbations using Monte Carlo sampling-based approximation and is defined as follows: sensitivity_eq In order to approximate sensitivity measure, by default, we sample from a sub-space of an L-Infinity ball with a default radius. The users can modify both the radius of the ball and the sampling function. More details about sensitivity measure can be found here:

Original paper